Petr_3D坐标生成

为了学习3D空间中的3D卷积特征，先通过将PSV变换到3D空间来建立3DGV。

PSV的坐标由(u,v,d)表示，其中（u,v）为像素坐标，d是深度，将其所在空间称为grid camera frustum space。深度坐标d按照预定的3D网络间距vd（深度单位）进行均匀采样，串联的信息能够使网络学习用来目标识别的语义特征

使用已知的相机内参，利用反向3D投影，在计算匹配损失前，将PSV最后的特征图从相机空间（u,v,d）到3D空间（x,y,z）：

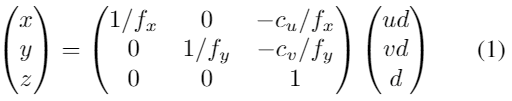
fx，fy为水平和垂直的焦距长度。

下图展示了转化过程，当物体识别在3D空间被学习，在相机frustum中施加了像素相关性约束（红虚线），在这两个表达中明显不同：

图3：volume变换：图像被成像平面采集（红实线），PSV在左侧camera frustum中将图像以等深度（蓝色虚线）投影，如世界空间（左图）和camera frustum space（中间）。相机空间中，车是失真的，由K的逆矩阵进行转换后，PSV被转换到3DGV，重新储存了车辆。

PSV中最后的特征图，low cost voxel（u,v,d）表示物体存在于光心与像素点（u,v）延长线的深度d的高概率。随着3D空间中的转换，low cost的特征表示这个voxle在场景前面，能够作为3D几何结构的特征为后面的3D网络所学习。

meshgrid coordinates：

类似于DGSN，首先对相机的视锥空间进行离散化，生成大小为的网格。网格中的每个点可以表示为,这里的是图像中的相机坐标，是沿与像平面正交的轴的深度值。例如，使用（50，30，64）大小的网络空间，如果有6个相机，那么grid meshgrid空间大小为.
3D coordinates

由于网络可以被不同的视图相机同时可视，对应的3D坐标空间中的3D点可以通过3D投影的逆变换进行计算：,这里的是第i个相机的内参矩阵，可以将3D空间点变换到相机视锥空间。

将内参矩阵拓展到meshgrid空间的维度。然后做meshgrid分支和内参分支相乘，这样得到3D空间维度为。