embedding
Input Embedding
前言
本文将针对 Transformer 关于输入部分的操作进行解析与总结,会结合代码来讲,只有结合了代码才比较“务实”,不然我总感觉很空洞、不踏实。
One-Hot Encoding
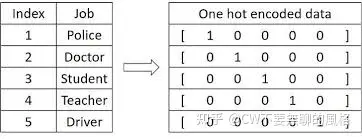
在 CV 中,我们通常将输入图片转换为4维(batch, channel, height, weight)张量来表示;而在 NLP 中,可以将输入单词用 One-Hot 形式编码成序列向量。向量长度是预定义的词汇表中拥有的单词量,向量在这一维中的值只有一个位置是1,其余都是0,1对应的位置就是词汇表中表示这个单词的地方。
例如词汇表中有5个词,第3个词表示“你好”这个词,那么该词对应的 one-hot 编码即为 00100(第3个位置为1,其余为0)
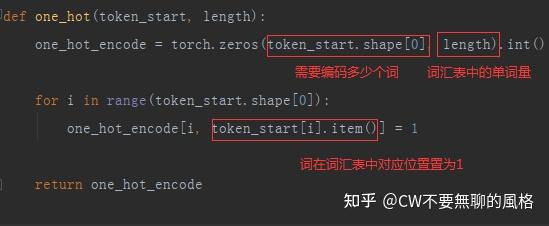
代码实现起来也比较简单:
Word Embedding
One-Hot 的形式看上去很简洁,也挺美,但劣势在于它很稀疏,而且还可能很长。比如词汇表如果有 10k 个词,那么一个词向量的长度就需要达到 10k,而其中却仅有一个位置是1,其余全是0,太“浪费”!
更重要的是,这种方式无法体现出词与词之间的关系。比如 “爱” 和 “喜欢” 这两个词,它们的意思是相近的,但基于 one-hot 编码后的结果取决于它们在词汇表中的位置,无法体现出它们之间的关系。
因此,我们需要另一种词的表示方法,能够体现词与词之间的关系,使得意思相近的词有相近的表示结果,这种方法即 Word Embedding。
那么应该如何设计这种方法呢?最方便的途径是设计一个可学习的权重矩阵 W,将词向量与这个矩阵进行点乘,即得到新的表示结果。
嗯?就这么简单吗?CW 告诉你:是的。为何能work?举个例子来看吧!
假设 “爱” 和 “喜欢” 这两个词经过 one-hot 后分别表示为 10000 和 00001,权重矩阵设计如下:
[ w00, w01, w02
w10, w11, w12
w20, w21, w22
w30, w31, w32
w40, w41, w42 ]那么两个词点乘后的结果分别是 [w00, w01, w02] 和 [w40, w41, w42],在网络学习过程中(这两个词后面通常都是接主语,如“你”,“他”等,或者在翻译场景,它们被翻译的目标意思也相近,它们要学习的目标一致或相近),权重矩阵的参数会不断进行更新,从而使得 [w00, w01, w02] 和 [w40, w41, w42] 的值越来越接近。
另一方面,对于以上这个例子,我们还把向量的维度从5维压缩到了3维。因此,word embedding 还可以起到降维的效果。
其实,可以将这种方式看作是一个 lookup table:对于每个 word,进行 word embedding 就相当于一个lookup操作,在表中查出一个对应结果。
在 Pytorch 框架下,可以使用 torch.nn.Embedding来实现 word embedding:
class Embeddings(nn.Module):
def __init__(self, d_model, vocab):
super(Embeddings, self).__init__()
self.lut = nn.Embedding(vocab, d_model)
self.d_model = d_model
def forward(self, x):
return self.lut(x) * math.sqrt(self.d_model)其中,vocab 代表词汇表中的单词量,one-hot 编码后词向量的长度就是这个值;d_model代表权重矩阵的列数,通常为512,就是要将词向量的维度从 vocab 编码到 d_model。
Position Embedding
经过 word embedding,我们获得了词与词之间关系的表达形式,但是词在句子中的位置关系还无法体现。
由于 Transformer 是并行地处理句子中的所有词,因此需要加入词在句子中的位置信息,结合了这种方式的词嵌入就是 Position Embedding 了。
那么具体该怎么做?我们通常容易想到两种方式:
1、通过网络来学习;
2、预定义一个函数,通过函数计算出位置信息;
Transformer 的作者对以上两种方式都做了探究,发现最终效果相当,于是采用了第2种方式,从而减少模型参数量,同时还能适应即使在训练集中没有出现过的句子长度。
计算位置信息的函数计算公式如下:
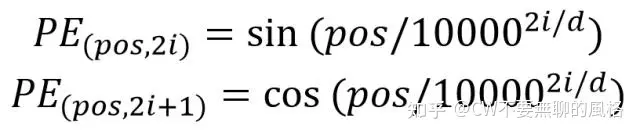
pos 代表的是词在句子中的位置,d 是词向量的维度(通常经过 word embedding 后是512),2i 代表的是 d 中的偶数维度,(2i + 1) 则代表的是奇数维度,这种计算方式使得每一维都对应一个正弦曲线。
为何使用三角函数呢?
由于三角函数的性质: sin(a+b) = sin(a)cos(b) + cos(a)sin(b)、 cos(a+b) = cos(a)cos(b) - sin(a)sin(b),于是,对于位置 pos+k 处的信息,可以由 pos 位置计算得到,作者认为这样可以让模型更容易地学习到位置信息。
为何使用这种方式编码能够代表不同位置信息呢?
由公式可知,每一维
i都对应不同周期的正余弦曲线: i=0时是周期为
综上可知,这种编码方式保证了不同位置在所有维度上不会被编码到完全一样的值,从而使每个位置都获得独一无二的编码。
Pytorch 代码实现如下:
class PositionalEncoding(nn.Module):
def __init__(self, d_model, dropout, max_len=5000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(p=dropout)
pe = torch.zeros(max_len, d_model) # max_len代表句子中最多有几个词
position = torch.arange(0, max_len).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2) *
-(math.log(10000.0) / d_model)) # d_model即公式中的d
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
pe = pe.unsqueeze(0)
self.register_buffer('pe', pe)
def forward(self, x):
x = x + self.pe[:, :x.size(1)] # 原向量加上计算出的位置信息才是最终的embedding
return self.dropout(x)实现过程中需要注意的一个细节是 —— self.register_buffer('pe', pe)* 这句,它的作用是将pe 变量注册到模型的 buffers()* 属性中,这代表该变量对应的是一个“持久态”,不会有梯度传播给它,但是能被模型的 state_dict 记录下来。
注意,没有保存到模型的 *buffers()* 或 *parameters()* 属性中的参数是不会被记录到state_dict 中的,在 *buffers()* 中的参数默认不会有梯度,*parameters()* 中的则相反。
通过代码可以看到,position encoding 是直接加在输入 x 上的,那么为何是相加而非拼接(concat)呢?拼接不是更能独立体现出位置信息吗?而相加的话都把位置信息混入到原输入中了,貌似“摸不着也看不清”..
这是因为 Transformer 通常会对原始输入做一个嵌入(embedding),从而映射到需要的维度,可采用一个变换矩阵做矩阵乘积的方式来实现,上述代码中的输入 *x* 其实就是已经变换后的表示,而非原输入。
OK,了解这一点后,我们开始尝试使用 concat 的方式在原始输入中加入位置编码:
给每一个位置
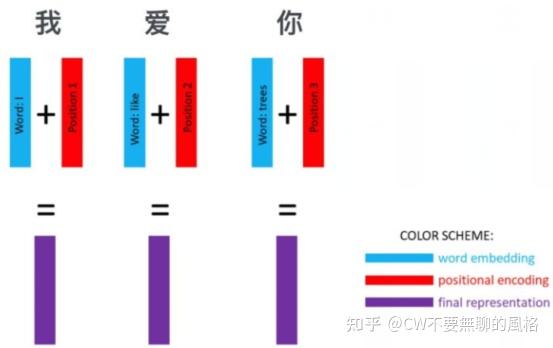
最后举个例子,Transformer 对输入的操作概括为如下: